Qualche tempo fa avevamo lavorato sulla proprietà associativa dell’addizione. E’ arrivato il momento di conoscere questa nuova regola:

Giochiamo con i nostri cubetti e costruiamo un parallelepipedo, come questo:

Quanti cubetti abbiamo usato per costruirlo? Ascoltiamoci un po’ tutti e tutte.
Le strategie personali, come sempre, sono diverse e ugualmente valide. Le risposte? variegate, dal corretto al meno corretto.
L’obiettivo è quello di lavorare sulla proprietà associativa, per questo propongo vari procedimenti.
1° procedimento:
Contiamo quanti sono i cubetti che si vedono sulla faccia superiore.
La faccia superiore è formata da 3 file di 4 cubetti ciascuna (o da 4 file di 3 cubetti ciascuna)

e i cubetti che si vedono sono in tutto 3×4 (o 4×3), cioè 12 cubetti.
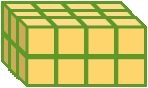
Ma il parallelepipedo è formato da due strati, ciascuno dei quali a sua volta è formato da 12 cubetti:

Perciò i cubetti in tutto sono il doppio, cioè 12×2, cioè 24
2° procedimento:
Contiamo adesso quanti sono i cubetti che formano una faccia laterale

Una faccia laterale è formata da 2 file di 4 cubetti ciascuna, in tutto quindi da 2×4 cubetti, cioè da 8 cubetti.
Ma il parallelepipedo è formato da 3 strati di 8 cubetti ciascuno.
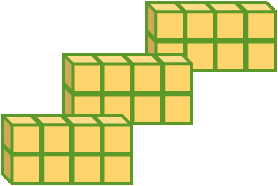
Perciò i cubetti devono essere 3 volte 8, cioè 3×8, cioè 24
3° procedimento:
Possiamo anche contare considerando un’altra faccia laterale formata da 3×2 cubetti

cioè da 6 cubetti
Ma il parallelepipedo è anche formato da 4 strati di 6 cubetti ciascuno

E in tutto contiamo sempre 24 cubetti
Possiamo anche usare dei diagrammi per descrivere i vari procedimenti:
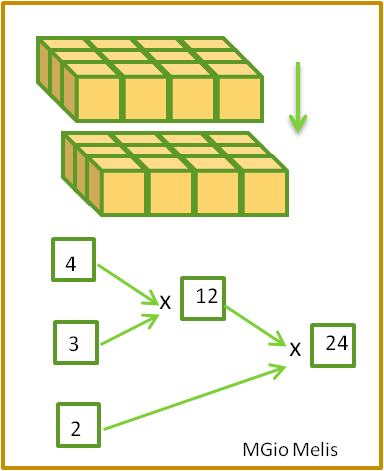
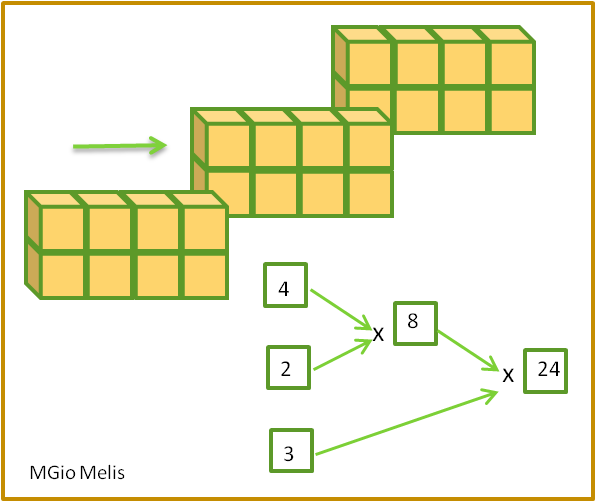
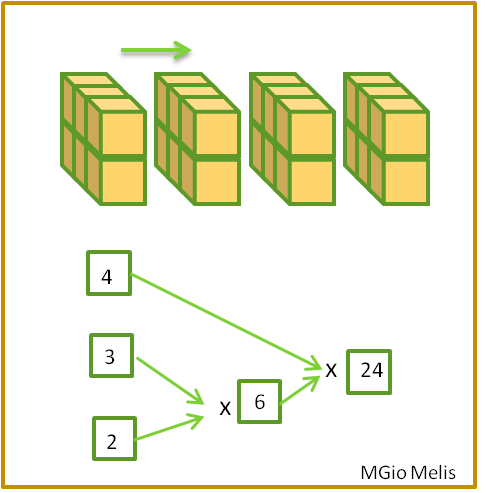
Gli schemi utilizzati ci permettono di osservare che anche associando i fattori in modi diversi, il prodotto ottenuto rimane sempre lo stesso. In questa attività, i cubetti che formavano il parallelepipedo erano sempre 24;
E questa proprietà della moltiplicazione è chiamata “proprietà associativa della moltiplicazione”
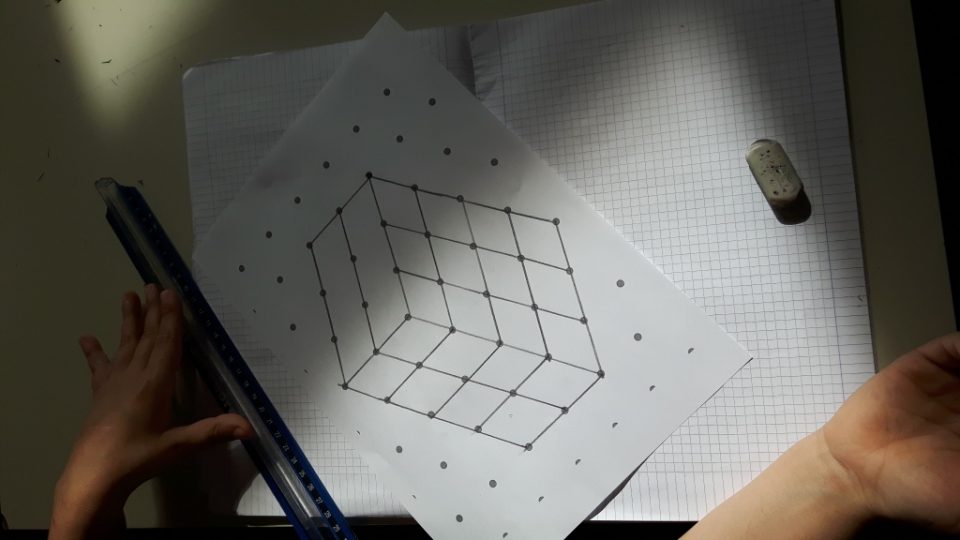
Ho poi consegnato delle copie di carta strutturata isometrica a puntini.
Nella prima, i puntini erano visivamente più grandi. Ciascuno/a doveva cercare di riprodurre il parallelepipedo iniziale. Ci sono stati diversi tentativi. Non è davvero così semplice, ma i risultati sono stati al di sopra delle aspettative.
Bravi e Brave




Nell’altra carta a puntini si dovevano costruire parallelepipedi diversi, a piacere. Alcuni hanno seguito l’istinto del momento e non sempre hanno rispettato la consegna. Non importa. Si sono esercitati e hanno creato figure geometriche comunque belle e originali:-)





E’ poi arrivato il momento di lavorare in gruppo considerando altri tre numeri, il 4, il 5, il 3. Nei gruppi si doveva costruire il parallelepipedo e applicare la proprietà associativa.
Ogni gruppo doveva calcolare quanti cubetti prendere per la costruzione del solido









Resta ancora da completare con qualche rifinitura:-)), ma l’attività può dirsi conclusa.
i bambini e le bambine della terza insieme alla maestra Maria Giovanna
da quel di SD

