Arriva il Natale! E le feste si colorano di luci
L’Albero di Natale crea atmosfere magiche, incantando con i suoi colori e i suoi addobbi, e decorando le nostre case e la nostra scuola.
È facile disegnare un albero; bastano un triangolo e un rettangolo.
Il nostro albero, quest’anno, è geometrico e anche aritmetico.
C’è il triangolo, sì, ed è un triangolo speciale: magico, come questi giorni di festa che verranno.
Ha tanti nomi questo triangolo. È figlio di tanti matematici. Noi lo abbiamo chiamato come uno di questi: Niccolò Fontana, detto il Tartaglia a causa della sua balbuzie


Qualche notizia storica
Ho chiamato il Triangolo dandogli il nome di un matematico italiano, ma non è proprio esatto.
Il triangolo infatti era conosciuto da Omar Khayyam (1.048-1.122) , da Niccolò Tartaglia, da Blaise Pascal e altri, e era già stato studiato dal matematico cinese Chia Hsien, nel 1.050 circa.
Il triangolo fece la sua apparizione in Europa nel 1.527, in un libro di aritmetica di Apianus.
Per costruirlo ci servono le addizioni:
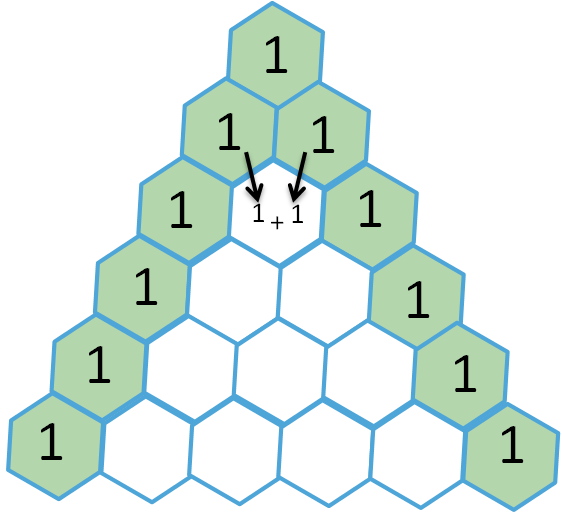
All’ inizio e alla fine di ogni riga c’è sempre 1
Inizia con le due righe superiori che sono 1, 1 e 1
Per trovare i numeri nella riga seguente, somma i due numeri
Un’ animazione:

Con la carta isometrica esagonale ciascuno/a costruisce il suo triangolo
È proprio osservando una delle griglie usate per costruire il triangolo, quella a maglie esagonali, che l’interazione in classe ha seguito un’altra direzione.
E tutto è partito da un’osservazione di Javier:
Era un’osservazione troppo “ghiotta“; non potevo farla cadere.
Ho chiesto perciò :- Secondo voi perchè le celle dei favi hanno questa struttura geometrica?
E queste le risposte:
Jana ha ben ricordato un’attività di misura di ampiezze angolari di qualche tempo fa:

e poi Mattia:
Bravi e brave.
State già iniziando a essere più consapevoli che le figure geometriche hanno riscontri concreti nella realtà che ci circonda e spesso sono direttamente collegate con la nostra vita.
Per quanto riguarda il mondo animale, un esempio è proprio quello di cui ha parlato Javier nel suo intervento.
Una bella struttura geometrica è data dalla forma delle celle di cui sono composti i nidi delle api.
Sono tutte di forma esagonale.

E’ più facile per tutti se facciamo qualche confronto.
Se confrontiamo la struttura esagonale delle celle con una struttura quadrata, disegnate entrambe su superfici di uguale estensione
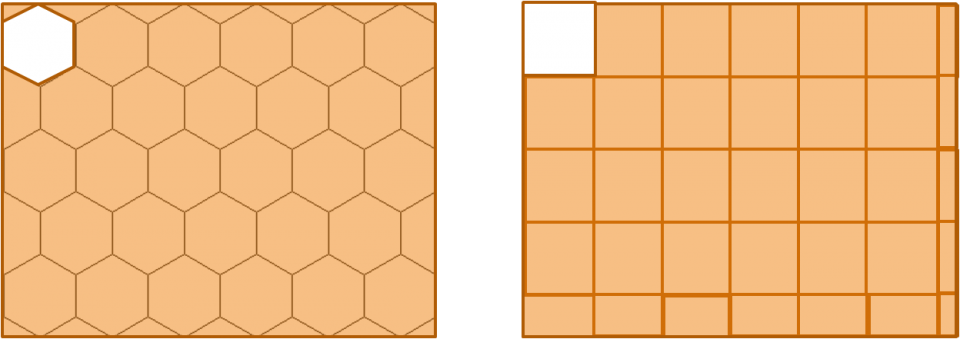
osserviamo che, a parità di grandezza, in uno stesso spazio, possono essere costruite più forme esagonali che quadrate.
Anche la forma pentagonale è poco pratica. Non solo il numero delle cellette che si possono formare è minore ; poi rimangono anche molti spazi inutilizzati

Con forme circolari:

Leggete questo breve brano tratto da:
Tane esagonali, da “L’architettura degli animali”, Mondadori, K. Von Frisch
“Le pareti delle celle di un favo, nella parte principale, sono disposte secondo prismi esagonali regolari. È questa la forma più razionale per la suddivisione di uno spazio in cui occorrano molti vani. È facile constatare che se le celle fossero, ad esempio circolari o pentagonali, ci sarebbero spazi inutilizzati; ci sarebbe perciò meno spazio utile e anche la necessità di costruire pareti staccate per ogni cella o almeno per alcuni lati di essa, con molto spreco di materiale.
Questi inconvenienti sarebbero eliminati con celle triangolari o quadrate ma, in questo caso, sarebbe necessario però più materiale per la loro costruzione perché i loro contorni, a parità di estensione, sono più lunghi di quelli delle cellette a forma esagonale.”
Voglio poi condividere questo filmato che ho trovato su Youtube e che fa al caso nostro. E’ in inglese… Solo maestra Tiziana ci potrà aiutare, ma le immagini vi serviranno:-)
Per adesso è tutto. Ma quante altre attività (alcune già iniziate) ci aspettano con questo triangolo magico.
dalla quarta di SD
e dalle maestre MariaGiovanna, Anna e Giulia:-)











Una piccola libera traduzione dell’ultimo video.
“Le api sono creature affascinanti per tante ragioni: la loro incredibile etica del lavoro, il dolcissimo sciroppo zuccheroso che producono e la loro intricata struttura sociale. Ma un’altra ragione è che le api, in realtà, sono eccellenti matematici. Gli scienziati affermano che questi minuscoli insetti possono calcolare angoli e capire la sfericità della Terra. Ma c’è un particolare genio matematico delle api dietro l’aspetto più importante della loro vita: l’alveare.
Come gli umani, le api hanno bisogno di cibo e di un rifugio per stare in vita. L’alveare non è solo la casa delle api, ma anche il posto dove depositano il miele. Dato che è così importante per la sopravvivenza, le api devono perfezionare la struttura architettonica dell’alveare. Se esamini ogni pezzo del favo, vedrai che è costruita da celle esagonali saldamente stipate. Di tutte le strutture possibili, perchè le api hanno scelto quella? Per capirlo, devi pensare come un’ape.
Le api hanno bisogno di un luogo sicuro per far vivere la loro colonia. E deve essere un luogo dove il loro nettare può essere immagazzinato e può maturare adeguatamente fino a diventare miele. Questo significa che c’è bisogno di una vera efficienza spaziale. Una buona soluzione è costruire piccole unità di stoccaggio, o celle, grandi abbastanza per farci stare un’ape e che possono essere contenitori in cui depositare il nettare. I barattoli del miele delle api.
Il prossimo passo è decidere di cosa saranno fatte le piccole celle. Le api non hanno becchi o braccia per raccogliere le cose, ma sono capaci di produrre cera. Il fatto è che produrla è tanto duro lavoro. Le api devono consumare 8 once (quasi 227 grammi) di miele per produrre 1 oncia (circa 28 grammi) di cera. Così non vogliono sprecarla. Hanno bisogno di una struttura che permetta loro di conservare la maggiore quantità di miele usando la minor quantità di cera.
Quale è questa forma/struttura? Immagina per un minuto che tutte le api debbano frequentare la facoltà di architettura e andare a lezione di matematica. Diciamo che chiedono al loro insegnante di geometria “Quale forma ci darebbe lo spazio maggiore per conservare il nostro miele, ma che richiede una minima quantità di cera?”. E poi l’insegnante di geometria risponde “La forma che cercate è il cerchio lasciando le api tornare al loro luogo di costruzione e iniziando a costruire un alveare usando celle circolari. Dopo poco alcune di loro potrebbero notare un problema con la loro struttura: piccoli buchi tra le celle. “Non possiamo neanche stare qui! Che spazio sprecato!” devono aver pensato. Così, ignorando la lezione di geometria e prendendo in mano la situazione, le api tornarono alla tavola da disegno per ripensare la struttura del loro alveare. Una suggerì i triangoli: “Possiamo usare i triangoli. Guardate! Si adattano insieme perfettamente.” Un’altra ape suggerì i quadrati. Alla fine, una terza ape alzò la voce per farsi sentire e disse: “I pentagoni non sembrano funzionare, ma gli esagoni sì! Vogliamo quella forma che ci farà usare la minor quantità di cera e potrà contenere la maggior quantità di miele. Sì, penso che sia l’esagono!”
“Perchè?”
“Sembra la più sferica delle altre forme”
“Ma come lo sappiamo con sicurezza?” Per scoprirlo, gli operosi insetti architetti hanno calcolato l’area del triangolo, del quadrato e dell’esagono e hanno trovato che l’esagono era, in realtà, la forma che dava loro il maggior spazio di deposito. Concordavano su una misura ideale e ritornarono a lavoro.
L’efficiente favo che è oggi un segno distintivo delle api, è probabilmente il risultato di prove ed errori, ma nel lungo periodo della storia evolutiva.
Comunque ha ripagato. Sbricia in un alveare con gli occhiali protettivi e la retina, naturalmente, e vedrai il risultato finale: un bellissimo favo compatto che nessun architetto può essere orgoglioso di aver progettato.”
🙂 Dalla parte delle api geometricamente attive.
Grazie, maestra Giulia, per questa efficace traduzione. Ti ringrazio tanto:-)Domani ne parleremo in classe.
Un abbraccio a te,
mgio