La supposizione di Goldbach e i numeri primi Gemelli

Con quest’altra attività, che amplia l’osservazione sui numeri primi (rivedi i lavori precedenti qui e qua ), scopriremo alcuni dei problemi non ancora risolti della storia della matematica.

Andiamo a passettini.

Ecco una griglia che contiene tutti i numeri primi minori di 100, che voi avete già osservato nel crivello di Eratostene

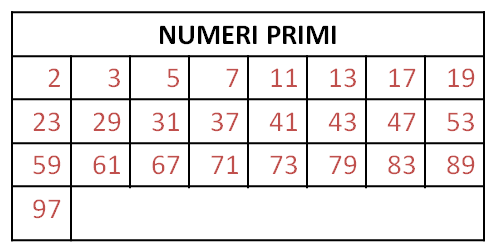
Abbiamo scoperto che a parte il 2

tutti gli altri numeri primi sono dispari.

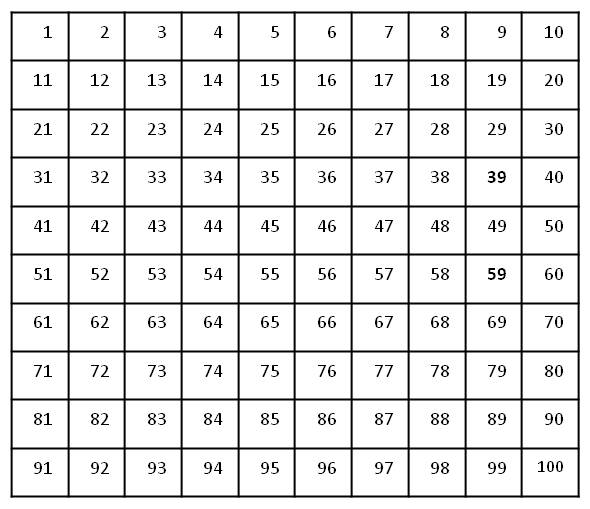
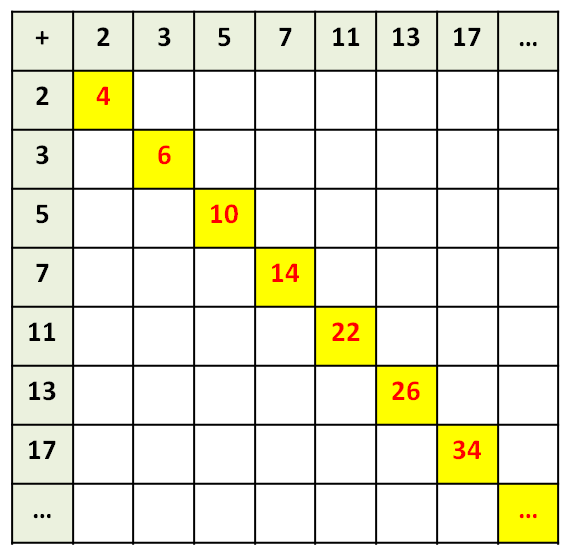
La  prima osservazione che possiamo fare è che  la somma di due numeri primi  è sempre un numero pari.

Con una tabella si vede chiaramente

• 

• 

Però possiamo chiederci:

È vero il contrario?

Cioè,  un numero pari è sempre la somma di due numeri primi?

Possiamo provare:

4, che è un numero pari, lo possiamo sommare con 2+2 che sono entrambi numeri primi;

6, sempre pari, può essere sommato con 3+3. 3 è un numero primo.

Anche 8: 3+5

E 10?

Con 10 possiamo trovare due modi diversi di sommare numeri primi:

5+5 e anche 3+7

È questa la famosa

“supposizione o congettura di Goldbach”

Dal vocabolario: “In matematica, la parola “congettura” indica una proposizione che è vera in certi casi e che si presume vera in ogni caso non essendo riusciti a dimostrare che in qualche caso è falsa.”.

Una “supposizione” è un’ipotesi incompleta, non ancora dimostrata.

E la sua storia ci porta indietro nel tempo.

Christian Goldbach (1690-1764) era un matematico tedesco in stretta corrispondenza epistolare (lettere😉), a quei tempi non esisteva WhatsApp 😊 ) con un altro matematico, Eulero, che noi già conosciamo (quello delle patate e dei diagrammi).

In una di queste lettere, Goldbach scriveva ad Eulero:

“ Tutti i numeri pari maggiori di 2 possono scriversi come la somma di due numeri primi.”

Leggiamo attentamente.

Eulero pensò bene a quanto gli aveva scritto il suo amico di penna e solo dopo aver provato, gli rispose con un’altra lettera scrivendogli che aveva verificato l’ipotesi sino al numero 1 000 e ancora in un’altra lettera sino al numero 2 500.

Sembrava che questa ipotesi reggesse. Sembrava .

Pensate, bambini e bambine,

che questa congettura ancora oggi non è stata dimostrata ed è considerata dalla comunità matematica uno dei problemi più complessi della storia della scienza.

È stata verificata con metodi informatici, con computer  potentissimi  per tutti i numeri pari inferiori a duemila miliardi.

Duemila miliardi?

Se pensiamo che duemila miliardi è il numero delle galassie del nostro universo ( una nuova ricerca infatti testimonia che l’universo contiene molte più galassie di quanto stimato finora. E non è una differenza da poco, secondo uno studio recente ci sarebbero 2mila miliardi di galassie, dieci volte in più di quanto si pensasse).
Il primo ”conteggio” delle galassie, utilizzando le foto del telescopio spaziale Hubble, aveva dato una cifra che si aggirava attorno ai 100-200 miliardi.) .

È facile vero dire a voce duemila miliardi, ma se noi lo scrivessimo come numero?

Solo per darvi un’idea visiva di questo numero, guardate questa tabella:

Ma la tabella sopra arriva fino alle centinaia di miliardi. Ed è già un numero enorme.

Duemila miliardi, allora?

Se mille miliardi ( si chiama un bilione) è 1 seguito da 12 zeri, duemila miliardi, il nostro numero, si scrive:

2. 000.000.000.000

Vedete quanto è lungaaaaa la sua scrittura in cifre?

Eppure dicendo “duemila miliardi” sembra cosa da poco😊

Questa supposizione tuttavia, come detto, non è stata ancora dimostrata ed è considerata dalla comunità matematica uno dei problemi più complessi della storia della scienza.

Vogliamo provarci insieme?

Nel quaderno costruite le due griglie di seguito

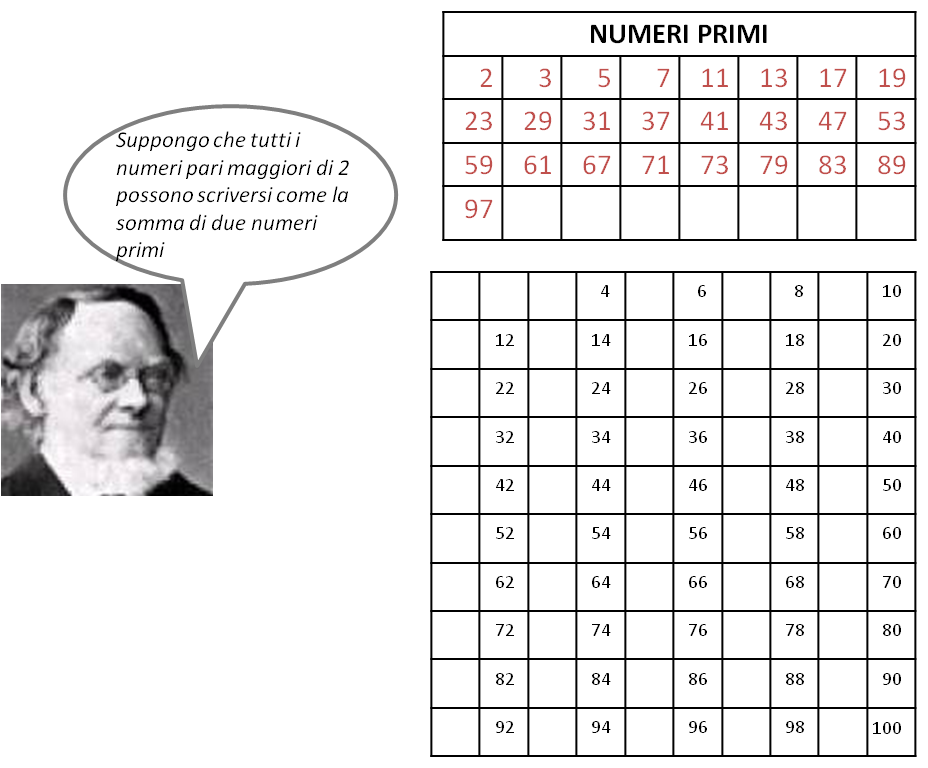
E iniziate a lavorare.

Partite dal 4

e continuate nel quaderno a trovare i due numeri primi che sommati diano numeri pari.

Aggiorno il post per inserire il contributo di Thomas che ho corretto proprio questo pomeriggio. A parte qualche piccolo e insignificante refuso, è stato SUPER. BRAVISSIMO❤

Avete osservato, bambini e bambine, come anche i matematici e qualunque persona si occupa di scienza in generale, per verificare delle loro ipotesi hanno bisogno di provare?

È così che si va avanti nelle conquiste. Con tentativi, errori, prove.

Alcune ipotesi possono poi essere provate, si parla allora di teoremi, altre hanno ancora bisogno di nuove e continue osservazioni e studi.

I numeri primi sono uno dei modelli che ancora resistono e mantengono segreti in relazione alla loro comparsa nella successione dei numeri naturali.

Appaiono così all’improvviso, senza ordine e senza uno schema generale che aiuti a rappresentarli.

Eppure i matematici hanno scoperto già da duemila anni che anche loro sono infiniti.

E un’altra curiosità, che testimonia gli sforzi dei matematici per scoprire qualcosa in più sui numeri primi, è data da quelli che vengono chiamati

Numeri primi gemelli

I Numeri  Primi GEMELLI si presentano come coppie di numeri dispari consecutivi

Anche questi si pensa siano infiniti, ma ancora non è stato dimostrato.

La prima osservazione da fare è che

Due numeri primi non possono essere consecutivi, dato che tutti i numeri primi sono dispari, e sappiamo che dopo un  numero dispari viene un pari, perciò non potrà mai essere numero Primo.

Quindi, per quanto vicini possano stare due numeri primi saranno sempre separati da due unità.

L’unica eccezione è rappresentata dal 2 e dal 3, che sono entrambi consecutivi e primi.

Fra i primi cento numeri troviamo le seguenti coppie di numeri primi separati da due unità.

Vi assicuro, sono molto poche le coppie di numeri primi gemelli; sono solo otto.

Io ve ne elenco alcune,

(3,5)

(5,7)

(11,13)

voi nel quaderno, completate.

E con quest’altra attività abbiamo ultimato i nostri lavori sui numeri primi.

Li affronterete ancora, anche quando sarete più grandi.

Buone supposizioni, perciò, e Buoni tempi a voi

in quel di SD

maestra Maria Giovanna